This calculus video tutorial shows you how to find the derivatives if inverse trigonometric functions such as inverse sin^1 2x, tan^1 (x/2) cos^1 (x^2) taDerivatives of Inverse Trigonometric Functions using First Principle Related questions Differentiate the following functions wrt x (i) cos − 1 (1 x 2 2 x )(i i) sin − 1 (2 x 1 − x 2 )The derivative of arctan x is denoted by d/dx(arctan(x)) and for complex values of x , the derivative is equal to 1/1x 2 for x ≠ i, i Integral For obtaining an expression for the definite integral of the inverse tan function, the derivative is integrated and the value at one point is fixed

What Is The Nth Derivative Of Arctan 2x 1 X 2 In Terms Of R And Theta Quora
Nth derivative of 2 tan inverse x
Nth derivative of 2 tan inverse x- · The Derivative of an Inverse Function We begin by considering a function and its inverse If \(f(x)\) is both invertible and differentiable, it seems reasonable that the inverse of \(f(x)\) is also differentiableWhat is the derivative of the following function, y = (tan − 1 x) 2 (x 3)?



If Y Tan 1 A X Log X A X A 1 2 Prove That Dy Dx 2a3 X4 Mention Each And Every Step Mathematics Topperlearning Com Yo8siu77
· Use the inverse function theorem to find the derivative of \(g(x)=\dfrac{x2}{x}\) Compare the resulting derivative to that obtained by differentiating the function directly Solution The inverse of \(g(x)=\dfrac{x2}{x}\) is \(f(x)=\dfrac{2}{x−1}\) We will use Equation \ref{inverse2} and begin by finding \(f′(x)\) Thus,The following prompts in this activity will lead you to develop the derivative of the inverse tangent function Let \(r(x) = \arctan(x)\text{}\) Use the relationship between the arctangent and tangent functions to rewrite this equation using only the tangent function Differentiate both sides of the equation you found in (a)Could there be another undiscovered function that is its own derivative, like e x ?
· Stack Exchange network consists of 177 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers Visit Stack ExchangeHome 1801 Chapter Section 2 Tools Index Up Previous Next Derivative of inverse tangent Calculation of Let f(x) = tan1 x then, · Y = Tan⁻¹ (x/a) The formul and follow this procedure dz/dx = 1/a substitute this and you will be able to prove that The formula for the nth derivative of y = arctan (x), is proved by induction
· Derivatives of Inverse Trigonometric Functions The following are the formulas for the derivatives of the inverse trigonometric functions `(d(sin^1u))/(dx)=1/sqrt(1u^2)(du)/(dx)` `(d(cos^1u))/(dx)=(1)/sqrt(1u^2)(du)/(dx)` `(d(tan^1u))/(dx)=1/(1u^2)(du)/(dx)` Example 2 Find the derivative of y = cos1 5x AnswerTive of the inverse of the tangent function y = tan−1 x = arctan x We simplify the equation by taking the tangent of both sides y = tan−1 x tan y = tan(tan−1 x) tan y = x To get an idea what to expect, we start by graphing the tangent function (see πFigure 1) The function tan(x) is defined for − π < x < 2 2 It's graph · tan−1 (2x1−x2)=2tan−1x So we are being asked for the nth derivative of 2tan−1x We are asked to find the answer in terms of r and θ but we are not given any definition of these terms The natural definitions would seem to be tanθ=x and r2=1x2



How To Differentiate Tan Inverse X By First Principle Quora
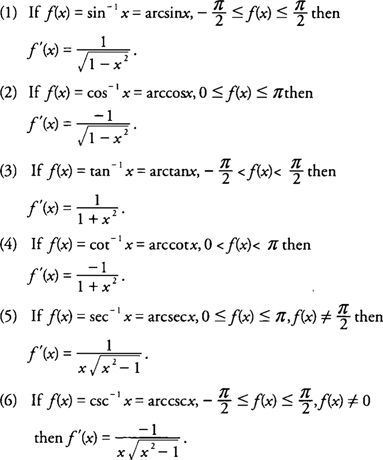


Differentiation Of Inverse Trigonometric Functions
· Question 1 Find the derivative of y = tan 1 (x 2) Solution Differentiating both side, we get Using the inverse derivative of tan1 θ = = Question 2 Find the derivative of y = sin 1 (3x2) Solution Differentiating both side, we get Using the inverse derivative of sin1 θ = = (3) = Question 3 Find the derivative of y = cos 1 (1 · Solution Let y = tan−12x tany = 2x Differentiating both side with respect to 'x' d dx (tany) = d dx (2x) ⇒ sec2y( dy dx) = 2 ⇒ dy dx = 2 sec2y ⇒ dy dx = 2 1 tan2y · The right hand side is a product of (cos x) 3 and (tan x) Now (cos x) 3 is a power of a function and so we use Differentiating Powers of a Function `d/(dx)u^3=3u^2(du)/(dx)` With u = cos x, we have `d/(dx)(cos x)^3=3(cos x)^2(sin x)` Now, from our rules above, we have `d/(dx)tan x=sec^2x` Using the Product Rule and Properties of tan x, we



Integration Of Tan 1 5x 1 6x 2 Dx Mathematics Topperlearning Com Zb45f7yy


How To Differentiate Y Tan 1 2x 1 X 2 For The Inverse Trigonometric Function Quora
Derivative of tan^2 (x)) full pad » x^2 x^ {\msquare} \log_ {\msquare} \sqrt {\square} \nthroot \msquare {\square} \le \geI have always seen the derivative of tan (x) as sec^2 (x) and the derivative of cot (x) as csc^2 (x) This seems to be the standard, and I have never seen it otherwise However, Sal is using 1/cos^2 (x) as the derivative of tan (x) and 1/sin^2 (x) as the derivative of cot (x)Using derivative, prove that tan –1x cot–1x = π2


What Is Tan Of 2 Tan Inverse 1 5 Quora


Find The Derivative Of Following Functions W R T X I Tan 1 A X 1 Ax Sarthaks Econnect Largest Online Education Community
Begin by setting y=arctan(x) so that tan(y)=x Differentiating both sides of this equation and applying the chain rule, one can solve for dy/dx in terms of y One wants to compute dy/dx in terms of x A reference triangle is constructed as shown, and this can be used to complete the expression of the derivative of arctan(x) in terms of xThe notations sin −1 (x), cos −1 (x), tan −1 (x), etc, as introduced by John Herschel in 1813, are often used as well in Englishlanguage sources —conventions consistent with the notation of an inverse function# Inverse tangent rule The inverse tan rule is given as y = tan1 (x) Formula tan1 (x) = tan1 (x), where x ∈ R Inverse tangent derivative The derivative of inverse tangent function is firstorder derivative It is given as dy/dx = 1 / 1 x 2


What Is The Derivative Of Y Tan 1 X Tan 1 1 X Quora



Differentiate Tan 1 Sqrt 1 X 2 X Wrt Cos 1 2xsqrt 1 X 2 If Xepsilon 1 Sqrt2 1 Youtube
· derivative of inverse tangent (2x) What is the derivative of arctan 2x? · Inverse Trigonometric Formulas Trigonometry is a part of geometry, where we learn about the relationships between angles and sides of a rightangled triangleIn Class 11 and 12 Maths syllabus, you will come across a list of trigonometry formulas, based on the functions and ratios such as, sin, cos and tanSimilarly, we have learned about inverse trigonometry concepts alsoFind the Derivative d/dx tan(x)^3 Differentiate using the chain rule, which states that is where and Tap for more steps To apply the Chain Rule, set as Differentiate using the Power Rule which states that is where Replace all occurrences of with The derivative of with respect to is



Formula For 2tan 1x And 3tan 1x


Solved 38 Show That Tan 1x Cos 2 Tan 1 X And The Chegg Com
Calculus, derivative of inverse tangent, Calculus, derivative of arctan(x),Calculus, derivative of tan^1(x)The derivative of the tan inverse function is written in mathematical form in differential calculus as follows ( 1) d d x ( tan − 1 ( x)) ( 2) d d x ( arctan ( x)) The differentiation of the inverse tan function with respect to x is equal to the reciprocal of the sum of one and x squared d d x ( tan − 1In the previous topic, we have learned the derivatives of six basic trigonometric functions sinx, cosx, tanx, cotx, secx, cscx In this section, we are going to look at the derivatives of the inverse trigonometric functions, which are respectively denoted as arcsinx, arccosx, arctanx, arccot x, arcsec x, arccsc x



If Y Tan 1 X 2 Show That X2 1 2 Y2 2x X2 1 Y1 2 Mathematics Shaalaa Com



Ex 7 2 18 Integrate E Tan 1 X 1 X 2 Ncert Maths
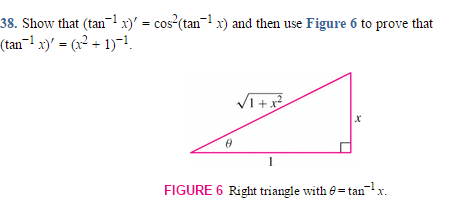
Finding the Derivative of the Inverse Tangent Function, $\displaystyle{\frac{d}{dx} (\arctan x)}$ The process for finding the derivative of $\arctan x$ is slightly different, but the same overall strategy is used Suppose $\arctan x = \theta$ Then it must be the case that $$\tan \theta = x$$ · \{\sec ^2}\left( {{{\tan }^{ 1}}x} \right) = 1 {\tan ^2}y = 1 {x^2}\ The derivative of the inverse tangent is then, \\frac{d}{{dx}}\left( {{{\tan }^{ 1}}x} \right) = \frac{1}{{1 {x^2}}}\Let y = tan(x) Recall the definition of tan(x) as sin(x)/cos(x) Therefore y = sin(x)/cos(x) Use the quotient rule, which states that for y = f(x)/g(x), dy/dx = (f'(x)g(x) f(x)g'(x))/g 2 (x) with f(x) = sin(x) and g(x) = cos(x) Recall the derivatives of sin(x) as cos(x) and cos(x) as sin(x)



Let F X 2tan 1x Sin 1 2x 1 X 2 Then



B1 6 Derivatives Of Inverse Trig Functions Ppt Download
Using the cosine inverse rule, d d x ( cot – 1 x) = – 1 1 x 2, we get d y d x = – 1 1 ( x a) 2 d d x ( x a) ⇒ d y d x = – 1 1 x 2 a 2 ( 1 a) ⇒ d y d x = – a 2 a 2 x 2 ( 1 a) ⇒ d y d x = – a a 2 x 2 ⇐ Derivative of Tangent Inverse ⇒ Derivative of Secant Inverse ⇒ · If by $\tan^{1}$ you mean the inverse function of the restriction of $\tan$ to the interval $(\pi/2,\pi/2)$, ie the function $\arctan$, you can apply the general formula for the derivative of an inverse function $$(\arctan)'(x)=\frac 1{(\tan)'(\arctan x)}==\frac 1{1\tan^2(\arctan x)}=\frac 1{1x^2}$$ · The Second Derivative Of sec^2x To calculate the second derivative of a function, differentiate the first derivative From above, we found that the first derivative of sec^2x = 2sec 2 (x)tan(x) So to find the second derivative of sec^2x, we need to differentiate 2sec 2 (x)tan(x) We can use the product and chain rules, and then simplify to find the derivative of 2sec 2 (x)tan(x) is 4sec 2


Differentiate Tan 1 1 X 2 1 X With Respect To Sin 1 2x 1 X 2 If 1 X 1 X 0 Sarthaks Econnect Largest Online Education Community


If Sin 1 2a 1 Cos 1 1 1 Tan 1 2x 1 X2 Where A X 0 1 Then The Value Of X Is Studyrankersonline
In doing this, the Derivative Calculator has to respect the order of operations A specialty in mathematical expressions is that the multiplication sign can be left out sometimes, for example we write "5x" instead of "5*x" The Derivative Calculator has to detect these cases and insert the multiplication sign · Find derivative of tan inverse of 2x/(1x^2) wrt cos inverse of (1x^2/1x^2) 1 answer below » Find derivative of tan inverse of 2x/(1x^2) wrt cos inverse of (1x^2/1x^2) Uncategorized Post navigation « Previous PostDerivative Calculator computes derivatives of a function with respect to given variable using analytical differentiation and displays a stepbystep solution It allows to draw graphs of the function and its derivatives Calculator supports derivatives up to



Update Ans Find Out The Derivative Of Tan 1 4 Rootx 1 4x With Respect To X



If Y Tan 1 X 1 Sqrt 1 X 2 Then Find Dy Dx
Turns out we don't really need to know f1 (x) If (4, 2) is a point on f1 (x), then (2, 4) is the point on f(x) at which f(x) has the reciprocal slope The green lines are tangent to the functions at those points They have reciprocal slope That means that the slope of the inverse at x = 4 can be found by taking the derivative of f(x) at x = 2All derivatives of circular trigonometric functions can be found from those of sin (x) and cos (x) by means of the quotient rule applied to functions such as tan (x) = sin (x)/cos (x) Knowing these derivatives, the derivatives of the inverse trigonometric functionsArcsin x Same goes for cos and tan Note Don't confuse sin1 x with (sin x)1They are different Writing sin1 x is a way to write inverse sine whereas (sin x)1 means 1/sin x Implicit Differentiation Implicit differentiation is a method that makes use of the chain rule to differentiate implicitly defined functions


What Is The Nth Derivative Of Tan 1 X Quora



Inverse Circular Function Study Material For Iit Jee Askiitians
This website uses cookies to improve your experience while you navigate through the website Out of these, the cookies that are categorized as necessary are stored on your browser as they are essential for the working of basic functionalities of the websiteProbably its sec(x) I'm giving solution taking secx(x) as sec(x) Sec(x)tan(x) =(1sin x)/cos x =(Cos x/2 sin x/2)/(cos x/2 sin x/2) =(Tan x/2 tanπ/4)/(1tan x * tan π/4) =Tan(π/4 x/2) So given equation becomes Tan¹(sec x tan x) =Tan¹(taJune 1, June 1, by admin Leave a Comment The general rule for derivate of arctan 2x is here, Let's take the derivative of arc tangent of 2x Now we can take the derivative with respect to x of Read More Search for Recent Posts


What Is The Nth Derivative Of The Tan Inverse 1 X 1 X Quora
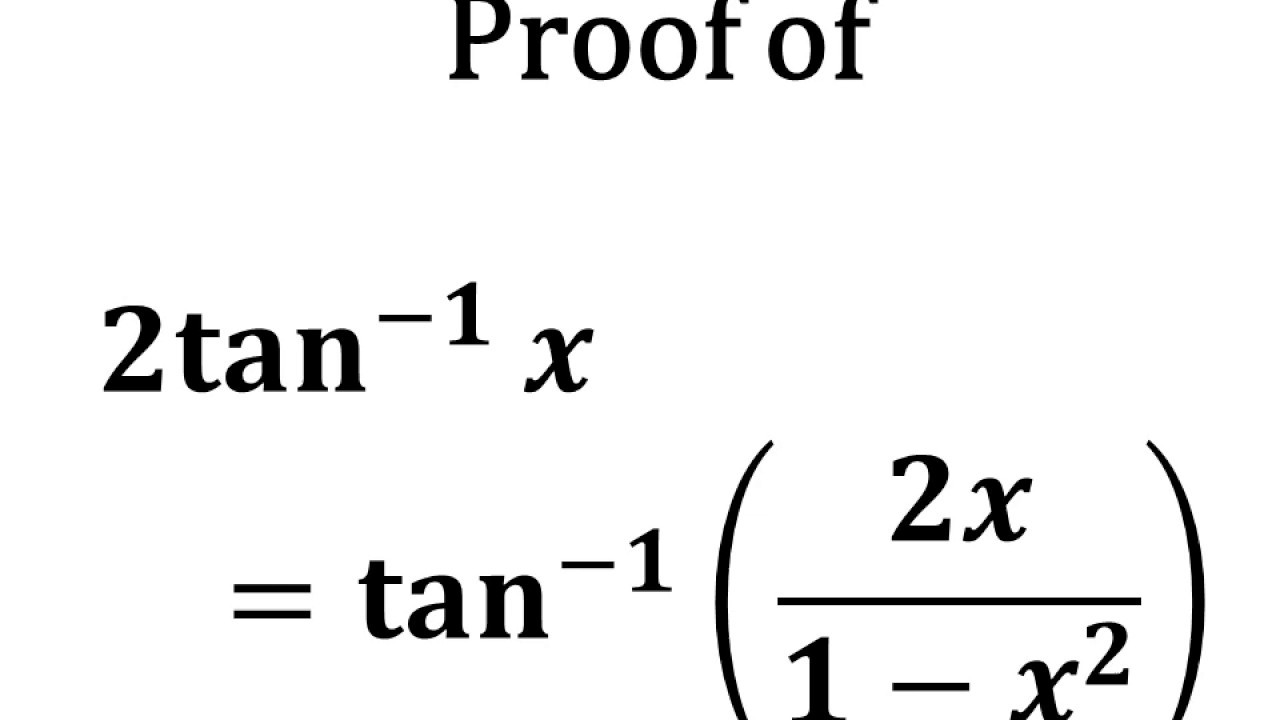


2tan 1 X Tan 1 2x 1 X 2 2arctan X Arctan 2x 1 X 2 Youtube
The function n p x= x1=n is the inverse of the function f(x) = xn where if nis even we must restrict the domain of fto be the set fx x 0g If nis odd, then f is onetoone on the whole real line Example Use the rule for the derivative of the inverse function to nd the derivativeExamples \frac {d^3} {dx^3} (\frac {3x9} {2x}) (\sin^2 (\theta))''' \frac {d^3} {dy^3} (a^y) \frac {d^3} {dx^3} (\frac {\sqrt {x}} {2x3}) \frac {d} {dx^3} (e^ {x^n}) (x\ln (x))''' thirdderivativeDerivative of Tangent Inverse In this tutorial we shall explore the derivative of inverse trigonometric functions and we shall prove the derivative of tangent inverse Let the function of the form be y = f ( x) = tan – 1 x By the definition of the inverse trigonometric function, y = tan – 1 x can be written as tan



Integration Of Tan Inverse X Ex 7 6 13 Chapter 7 Class 12



Misc 13 Solve 2 Tan 1 Cos X Tan 1 2 Cosec X Miscellaneous
· Here are the steps for deriving the arctan(x) derivative rule 1) y = arctan(x), so x = tan(y) 2) dx/dyx = tan(y) = sec 2 (y) 3) Using sum of squares corollary sec 2 (y) = 1 tan 2 (y) 4) tan 2 (y) = x 2 so dx/dy = 1 x 2 5) Flipping dx/dy, we get dy/dx = 1/(1 x 2)What is the derivative of a x 2 2 h x y b y 2


Derivatives Of Inverse Trigonometric Functions



Find The Second Order Derivatives Of The Function Tan 1 X Mathematics Shaalaa Com


What Is The Differentiation Of Sin 2 Tan 1 1 X 1 X Quora



Lesson 12 Derivative Of Inverse Trigonometric Functions


How To Find The Derivative Of F X Tan 2 3x 2 Quora



Differentiate The Following W R T X Tan 1 X 1 6x 2 Cot 1 1 10x 2 7x



Solved Find The Derivative I F X X 2 Tan 1 X 1 Chegg Com



What Is The Nth Derivative Of Arctan 2x 1 X 2 In Terms Of R And Theta Quora



Show That Z Ln X 2 Y 2 2 Tan 1 Y X Satisfies The Laplaces S Equation Mathematics Stack Exchange



Derivative Of Tan Inverse With Chain Rule Youtube
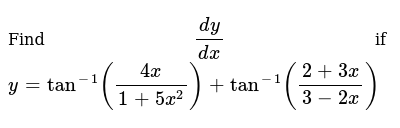


Find Dy Dx If Y Tan 1 4x 1 5x 2 Tan 1 2 3x 3 2



Differentiate Tan 1 1 X2 1 2 1 X Wrt Sin 1 2x 1 X2 Explain In Great Detail Mathematics Topperlearning Com Yx862gdd
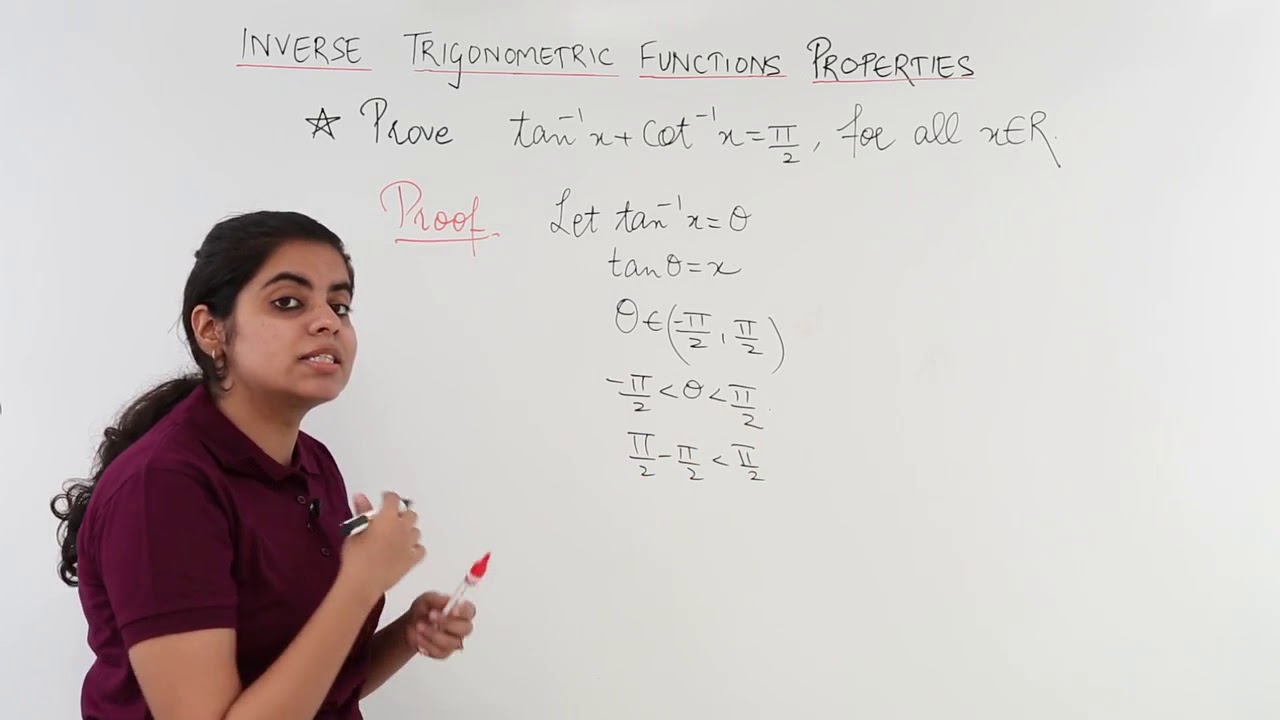


Prove Tan Inverse X Cot Inverse X Pie 2 Youtube


Show That 2tan 1 Tan A 2 Tan P 4 B 2 Tan 1 Sina Cosb Cosa Sinb Sarthaks Econnect Largest Online Education Community



The Derivative Of Tan 1 Sqrt 1 X 2 1 X W R T Tan 1x Is Youtube



Integration Of Tan Inverse X Ex 7 6 13 Chapter 7 Class 12


Prove That Tan 1 1 X2 1 X2 1 X2 1 X2 P 4 1 2 Cos 1x2 Studyrankersonline
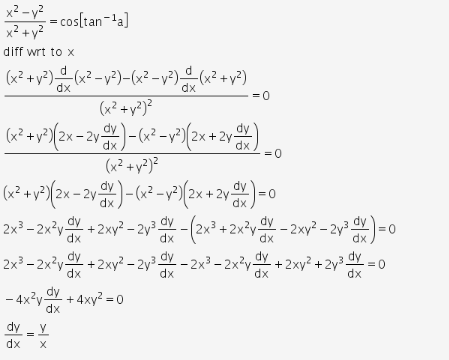


If Cos 1 X2 Y2 X2 Y2 Tan 1 A Prove That Dy Dx Y X Cbse Class 12 Learn Cbse Forum
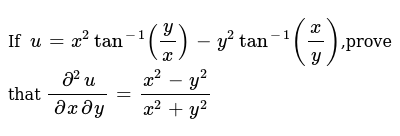


If U X 2tan 1 Y X Y 2tan 1 X Y Prove That Del 2u Delxde



Solved Compute The Derivatives Of The Inverse Trigonometr Chegg Com



Second Derivative Of Tan 2x Youtube



Ques No 3 Solve The Nth Derivative Showing Step By Step Procedure Mathematics Topperlearning Com 0x2t7zpp



Ex 5 3 9 Find Dy Dx In Y Sin 1 2x 1 2x2 Chapter 5



Partial Derivative If U X 2 Tan 1 Y X Y 2 Tan 1 X Y Prove ә 2u әxәy X 2 Y 2 X 2 Y 2 Youtube



Ex 5 7 8 Find Second Order Derivatives Of Tan 1 X Ex 5 7



Differentiate W R T I X Tan Inverse A X 1 Ax Brainly In


What Is The Value Of Dy Dx If Y Tan 1 4 X 1 4x Quora



41 If Y Sin 2tan 1 Root Over 1 X 1 X Find Dy Dx Maths Continuity And Differentiability Meritnation Com



Tan Inverse 2x 1 X Square Cot Inverse 1 X Square 2x 2pi 3 Brainly In



If Y E X Tan Inverse X Prove That D1 X 2 D 2y Dx 2 2 1 X X 2 Dy Dx 1 X 2 Y 0 Maths Application Of Derivatives 1415 Meritnation Com
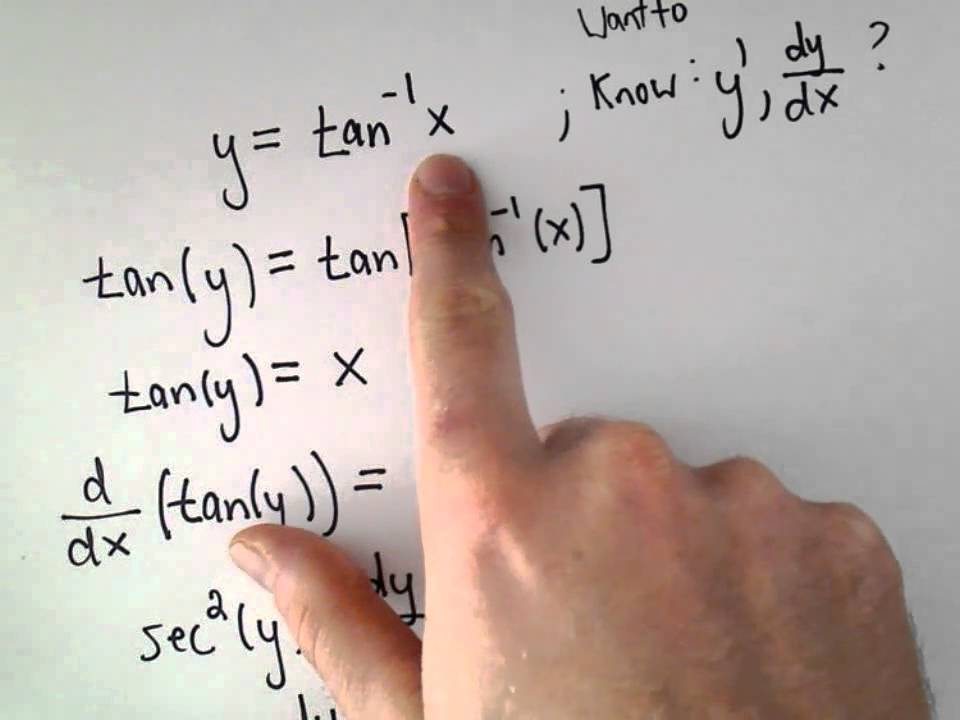


Deriving The Derivative Of Inverse Tangent Or Y Arctan X Youtube



Find The Nth Derivative Of Tan Inverse X Upon A Brainly In



Inverse Trigonometric Functions Class 12 Notes Maths Chapter 2 Learn Cbse Class12mathsnotes Inver Trigonometric Functions Math Formula Chart Class 12 Maths



Find The Sum Tan 1 X 1 1 2x 2 Tan 1 X 1 2 3x 2 Tan



Differentiate Tan 1 1 X 2 X W R T Cos 1 2x 1 X 2 When X 0


How To Differentiate With Respect To X Of Sin 1 Cosx Tan 1 Cotx Quora



Differentiate Tan 1 X 1 X 2 With Respect To Sin 1 2x 1 X 2



Differentiate The Following W R T X Tan X A 2 X 2
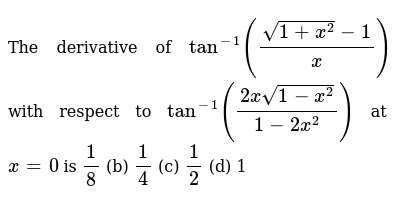


The Derivative Of Tan 1 Sqrt 1 X 2 1 X With Respect To Tan



Prove That Ddx 2xtan 1x Log 1 X 2 2xtan 1x



Derivatives Of Inverse Trigonometric Functions Sin 1 2x Cos 1 X 2 Tan 1 X 2 Sec 1 1 X 2 Youtube



Pi 2 Tan Inverse X Let F X 3 X 2 Tan Pie X 2 Find F 1 Inverse Of 3 And F F 1 Inverse 5



If Tan 1 X2 Y2 X2 Y2 A Prove That Dy Dx X 1 Tana Y 1 Tana Brainly In


Derivative Of Inverse Tangent



If Y Tan 1 X 1 Sqrt 1 X 2 Then Find Dy Dx


Prove Tan 1 X Frac 1 1 X 2 Mathematics Stack Exchange


What Is The Nth Derivative Of Tan 1 X Quora



If Y Sec Tan 1 X Then Dy Dx Is Youtube



Prove That D Dx 2x Tan 1 X Log 1 X 2 2 Tan 1 X


The Differential Coefficient Of Tan 1 2x 1 X 2 With Respect To Sin 1 2x 1 X 2 Is Sarthaks Econnect Largest Online Education Community



If Y Tan 1 A X Log X A X A 1 2 Prove That Dy Dx 2a3 X4 Mention Each And Every Step Mathematics Topperlearning Com Yo8siu77



If Log X 2 Y 2 Tan 1 Yx Then Prove That Dydx X Yx Y


Find The Value Of 4 Tan 1 1 5 Tan 1 1 239 Studyrankersonline



Y Tan 1 Sqrt 1 X 2 Sqrt 1 X 2 Sqrt 1 X 2 Sqrt 1 X 2 W H E R E 1 Ltx Lt1 X 0 Youtube



Integrate X 2 Tan 1 X Dx Youtube



Derivative Of Tan Inverse 2x



Ex 7 2 18 Integrate E Tan 1 X 1 X 2 Ncert Maths


How To Find The Nth Derivative Of Math Tan 1 X Math Quora



Derivative Of Inverse Tangent Video Khan Academy



Proof First Of 2 Tan Inverse X Youtube



How To Solve Tan 1 2x 1 X2 Cot 1 1 X2 2x Pie 3 Brainly In



If U X 2tan 1 Y X Y 2tan 1 X Y Then Find 2u X Y


What Is The Integration Of Tan Inverse X Quora


What Is The Differentiation Of Sec Inverse Tan 2x Quora


Question Video The Derivative Of An Inverse Tangent Function Nagwa



Example 27 Find Derivative Of F X Tan 1 X Class 12



Lim X Oo Pi 2 Tan 1 X 1 X Is Equal To


Show That 2tan 1 Tan A 2 Tan P 4 B 2 Tan 1 Sina Cosb Cosa Sinb Sarthaks Econnect Largest Online Education Community



Find The Derivative Of Tan 1 X Wrt To Cot 1 X Brainly In


What Is The Derivative Of Tan 1 Sec X Tan X Quora



Tan1 2 Sin 1 2x 1 X 2 Cos 1 1 Y 2 1 Y 2 X Y 1 Xy If X Lt 1 Y Gt 0 And Xy Gt 1 Mathematics Topperlearning Com Exkwfcdd



Ex 5 7 17 If Y Tan 1 X 2 Show X2 1 Y2 2x X2 1



Derivative Of Inverse Tan X By First Principle Method Youtube



Prove First Of Tan Inverse X Tan Inverse Y Youtube
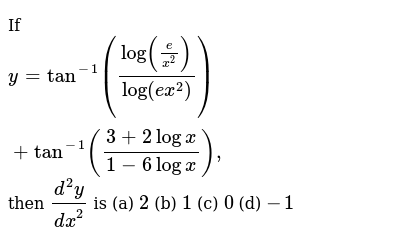


If Y Tan 1 Log E X 2 Log Ex 2 Tan 1 3 2logx 1 6logx



0 件のコメント:
コメントを投稿